Pred 372 rokmi stál francúzsky matematik Pierre de Fermat pri zrode pravdepodobne najväčšej výzvy v dejinách matematiky.
Prišiel s problémom, ktorý sa pokúšali vyriešiť v podstate všetci významní matematici posledných storočí, a každý z
nich neuspel. Dnes, 1. apríla, od 00:00 do 20:00, bol vyriešením tohto problému podmienený prístup na našu stránku.
Predhodili sme vám jeden z najneriešiteľnejší problémov histórie. Potešilo nás, ako ste sa ho mnohí zanovito pokúšali
za pár hodín vyriešiť. Nachytali sme vás, veď dnes bol 1. apríl :)
Aké "riešenia" a reakcie ste nám poslali vám rozpovieme v tomto článku.
1. apríl
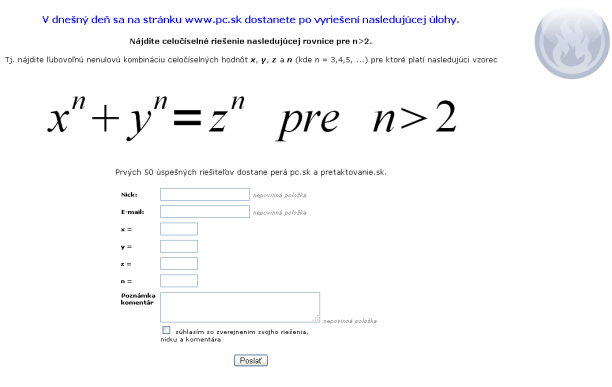
Návštevníkov www.pc.sk a www.pretaktovanie.sk dnes od polnoci na titulke čakala táto úloha, ktorá podmieňovala prístup na stránku
Záloha stránky s úlohou.
Táto úloha je legendou histórie matematiky. Začnime ňou, vaše riešenia a reakcie prídu na rad hneď po nej.
Začiatok príbehu - troška matematiky nikoho nezabije
Najskôr sa však pozrime na to čo sme vám to dnes predostreli, a odkiaľ sa to vzalo. Problém ktorý ste včera mnohí riešili v snahe dostať sa na stránku pochádza z pera matematika Pierre de Fermata a medzi matematikmi je známy asi ako Rosewell medzi priaznivcami záhad.
Pierre de Fermat bol francúzsky právnik, ktorý sa matematikou zaoberal ako svojim koníčkom. Spomedzi vecí ktorými prispel k rozvoju matematiky medzi najvýznamnejšie patrí položenie základov teórie pravdepodobnosti (spolu s Blaise Pascalom), objavenie metódy hľadania extrémov kriviek (priamu predchodkyňu rovnakej metódy diferenciálneho počtu) a samozrejme jeho pôsobenie v oblasti teórie čísel. Sám seba nazýval amatérom a väčšinu svojich objavov popísal len v listoch svojim priateľom, pričom ich zväčša nedoložil žiadnym dôkazom, prípadne ho len naznačil. Tento jeho "zvyk" nedokazovať svoje objavy stál pri koreňoch jedného z najchytľavejších príbehov v dejinách matematiky. Skôr než si popíšeme jeho vznik, pozrime sa na trošku matematiky.
Každý pozná Pytagorovu vetu, ktorá v matematickom zápise vyzerá nasledovne
Ak budem hľadať jej možné riešenia v ktorých sú a, b a c celé čísla, zistíme, že ich už po pomerne krátkom skúmaní nájdeme viacero. Napríklad to môžu byť kombinácie a = 3, b = 4, c =5 či a = 5, b = 12, c = 13
Takýmto trojiciam čísel sa hovorí Pytagorejské trojice a v skutočnosti je ich nekonečné množstvo.
Spýtajme sa či je možné nájsť podobné trojice celých čísel pre rovnicu
alebo pre rovnicu
alebo všeobecne povedané pre rovnicu
Toto je otázka nad ktorou rozmýšľal Fermat pri štúdiu latinského prekladu starogréckej zbierky algebraických príkladov, slávnej Diofantovej Aritmetiky. Prišiel s odpoveďou, že to možné nie je. A tvrdil že to vie aj dokázať.
Ako sme už spomenuli, mnoho svojich objavov nedoplnil dôkazom. A tak aj pri skúmaní úloh Diofantovej Aritmetiky si k úlohe zaoberajúcej sa hľadaním Pytagorejských trojíc len pripísal na okraj knihy, poznámku:
Nie je možné rozdeliť kocku do dvoch kociek, či štvrtú mocninu do dvoch štvrtých mocnín alebo všeobecne akúkoľvek mocninu vyššiu ako druhú do dvoch rovnakých mocnín. Objavil som naozaj zvláštny dôkaz tohto tvrdenia, no okraj tejto knihy je primalý na to, aby sa tam vošiel.
Popis dôkazu či len náznak aký dôkaz to bol sa nikdy nenašiel. Vieru že Fermat dôkaz skutočne mal mala na svedomí jeho reputácia fenomenálneho matematika, ktorý podobné tvrdenia bez dôkazu uvádzal bežne, pričom tieto sa neskôr ukázali ako pravdivé. Takýchto tvrdení, spomínajúcich že pozná dôkaz, či len s náznakom ako dôkaz vykonať bolo v komentároch ktoré napísal na okrajoch jeho výtlačku Diofantovej Aritmetiky vyše 20. Všetky boli správne, a všetky boli postupne v relatívne krátkom čase dokázané až na jediné, až na spomenutý problém neexistencie riešenia rovnice a^n + b^n = c^n pre n väčšie ako 2. Tak vzniklo označenie Posledná Fermatova veta. Takto je nazývaná v anglickej literatúre (Fermat's Last Theorem) u nás jej hovoríme Veľká Fermatova veta.
Fermat vytvoril vetu (úlohu), ktorej formulácia je veľmi jednoduchá. Jej dokázanie sa však ukázalo byť viac než zložité a hoc k nemu mnohí prispeli svojou troškou, definitívne riešenie na seba nechalo dlho čakať. Problémom sa zaoberali napríklad Euler, Dirichlet či Legendre ale na dôkaz neprišli. Ako ubiehali roky a ako sa počet tých ktorí sa Fermatovou vetou neúspešne zaoberali zväčšoval, tak rástla výzva a prestíž ktoré jej úspešné vyriešenie sľubovalo.
Mimochodom, ide o úlohu s najväčším počtom nesprávnych riešení v histórii matematiky. A to riešení nielen od matematikov. O jej riešenie sa pokúšali aj tisícky nadšencov, keďže sa predpokladalo, že úloha je riešiteľná matematickými metódami 17. storočia a riešenie je pomerne krátke. Táto pomerná "dostupnosť" a ohromná prestíž ktorá čakala na objaviteľa dôkazu nedala mnohým spať.
Cesta ktorou sa dokazovanie Veľkej Fermatovej vety uberalo je naozaj dlhá, dramatická a spletitá. Tým aj mimoriadne zaujímava, no bohužiaľ niet tu naň miesta, Môžem však skutočne odporúčať knihu Simon Singh - Velká Fermatova věta (Academia, 2007) - http://www.martinus.sk/?uItem=35773 ,ktorá tento príbeh vynikajúco zaznamenáva.
Po tri a pol storočí Veľkú Fermatovu vetu nakonies s pomocou matematiky druhej polovice dvadsiateho storočia dokázal v roku 1994 britský matematik Andrew Wiles. Jeden s najlepších matematikov súčasnosti, strávil jej riešením, v tajnosti, 7 rokov (túto časť, toto finále príbehu Veľkej Fermatovej vety zaznamenáva vynikajúci dokument ktorý pre BBC natočil Simon Singht, autor vyššiespomenutej knihy - dokument si môžete pozrieť na tomto linku: http://video.google.com/videoplay?docid=8269328330690408516). Wilesov dôkaz je extrémne zložitý a dlhý (viď. http://math.stanford.edu/~lekheng/flt/wiles.pdf) a používa metódy enormne vzdialené od tých ktoré mohol poznať Pierre de Fermat. Z toho sa zväčša usudzuje, že Fermat žiaden dôkaz nemal, prípadne že mal chybný dôkaz.
Ale, v mnohých predsa len ešte ostal červík pochybností. Čo ak? Čo ak krátky a jednoduchý dôkaz predsa len existuje.
Naďalej ho mnohí hľadajú.
Ako ste riešili
Reakcie na 1.aprílový žart boli rôzne, od veľmi pozitívnych po veľmi negatívne. Tých negatívnych začalo ubúdať, potom ako s príchodom dnešného rána mnohým začalo dochádzať aký je to dnes deň.
Celkovo sme zaznamenali viac než tisíc pokusov o riešenie ktoré sa delili do nasledujúcich skupín.
1. Úspešné riešenia v tom zmysle že riešitelia vedeli že ide o Veľkú Fermatovu vetu. Vedeli to alebo to vygooglili.
Častokrát sa objavovali kvázisprávne riešenia ako napríklad:
3987^12 + 4365^12 = 4472^12
6,3976656349698612616236230953154e+43 - ľavá strana rovnice 6,3976656348486725806862358322169e+43 - pravá strana rovnice
Ako vidíte, zhoduje sa len prvých 10 miest oboch čísel. Kalkulačka vám ukáže rovnaké čísla, vďaka zaokrúhleniu, ale správne riešenie to nie je. Ide o slávne riešenie ktoré sa objavilo v sitcome Simpsonovci a odvtedy putuje svtom :)
Príjemnýn prekvapením bolo pre nás neznáme kváziriešenie užívateľa hankie (zdroj D. J. Bernstein (July 29, 2001) http://cr.yp.to/threecubes.html)
x = -2901096694
y = -15550555555
z = 15584139827
n = 3
3784848573216710602200773002259 - ľavá strana rovnice
3784848573216710602200773002283 - pravá strana rovnice
Prvých 29 číslic je rovnakých.
V tejto skupine bolo najviac tých ktorí ocenili tento žart. Prvých 50 čitateľov ktorí spoznali že ide o Veľkú Fermatovu vetu dostane od nás sľúbené pero pc.sk a pretaktovanie.sk
Zoznam výhercov :
1). prvým bol krátko po polnoci yesper, ktorý správne napísal "riesenie tejto rovnice podla velkej fermatovej vety neexistuje, samozrejme v mnozine prirodzenych cisel"
2). pEpinko
3). matko86
4). Shigi
5). Lukasko^
6). shigi
7). drahomir.s
8). HellAngel
9). rottenkiwi
10). lukasko
11). zwARO
12). matko86
13). lucky
14). pepe
15). kyleah
16). dmitrijj
17). gabiX
18). spermi
19). avixe
20). Velyger
21). Michal
22). mosqa
23). PROMETHEUS
24). pal0
25). janci2
26). Nightlight
27). Leteku
28). peYko
29). nexus33
30). jatmz
31). louth
32). predator
33). latigi
34). Thunderbolt
35). pacho666
36). ddussann
37). mirak
38). Maxx
39). frcko
40). Tom.raketa
41). risomas
42). Blackhawk
43). edt
44). matej1982
45). powerarm
46). Seky
47). mastro
48). gyver
49). Phalanx
50). chosefina
2. Riešitelia pokúšajúci sa nájsť riešenie. Mnohí z nich pochopili že rovnica má nulové riešenie, to však zadanie vylučovalo. Postupne intuitívne pochopili že pôjde o nejaký žart, alebo že rovnica asi riešenie mať nebude.
3. Tí ktorí to vzdali hneď na začiatku
4. Nahnevaní čitatelia. Sme radi že pozitívne reakcie prevažovali, ale pár nahnevaných reakcií stálo za to.
Napríklad :
Užívateľ lordjustice a jeho poznámka: "Komentár je ten, že kto vymyslel túto hovadinu, tak by nemal dostať výplatu!!!". Milý lord spravodlivosti, chceme Ťa uistiť, že za tento nápad, jeho prípravu, či za tento článok nik honorár nedostane :)
5. Srandisti a tí ostatní
Informatik sa nezaprel: baqq:
x = 8
y = 8
z = 10
n = 3
Poznamka: 512+512 = sice 1024, ale v bitoch je to 1000, cize 10 na 3.
Anonym: Poznamka: Kdybych tohle umel vyresit, tak nechodim na pc.sk. ;-)
My dodáme, že súhlasíme, že dokazat Fermatovu vetu vie len zopar ľudí na svete a je to úctyhodný výkon. Taký čo to, vie by kvoli Porche, jachte na ceste okolo sveta a frajerke čo vyhrala miss minulý rok nemal mať na pc.sk čas :)
lamzalo fermat by sa v hrobe obracal ze ho zneuzili na prvy april :-D
fawrell - potom čo správne vysvetlil že riešenie neexistuje poznamenal "S googlom sa stal zivot prilis lahkym. Jedina vec na uvazovanie bola, ako zadat do googla "x na n-tu". Ale s tym si iste poradila vacsina ludi. Dalej je to uz len o googli. Co by ludia robili bez googla ..."
Tak, hádam aj tí nahnevaní majú tú trošku zmyslu pre humor, a tento náš 1. apríl nejako strávia :)
1. apríl
Návštevníkov www.pc.sk a www.pretaktovanie.sk dnes od polnoci na titulke čakala táto úloha, ktorá podmieňovala prístup na stránku
Záloha stránky s úlohou.
Táto úloha je legendou histórie matematiky. Začnime ňou, vaše riešenia a reakcie prídu na rad hneď po nej.
Začiatok príbehu - troška matematiky nikoho nezabije
Najskôr sa však pozrime na to čo sme vám to dnes predostreli, a odkiaľ sa to vzalo. Problém ktorý ste včera mnohí riešili v snahe dostať sa na stránku pochádza z pera matematika Pierre de Fermata a medzi matematikmi je známy asi ako Rosewell medzi priaznivcami záhad.
Pierre de Fermat bol francúzsky právnik, ktorý sa matematikou zaoberal ako svojim koníčkom. Spomedzi vecí ktorými prispel k rozvoju matematiky medzi najvýznamnejšie patrí položenie základov teórie pravdepodobnosti (spolu s Blaise Pascalom), objavenie metódy hľadania extrémov kriviek (priamu predchodkyňu rovnakej metódy diferenciálneho počtu) a samozrejme jeho pôsobenie v oblasti teórie čísel. Sám seba nazýval amatérom a väčšinu svojich objavov popísal len v listoch svojim priateľom, pričom ich zväčša nedoložil žiadnym dôkazom, prípadne ho len naznačil. Tento jeho "zvyk" nedokazovať svoje objavy stál pri koreňoch jedného z najchytľavejších príbehov v dejinách matematiky. Skôr než si popíšeme jeho vznik, pozrime sa na trošku matematiky.
Každý pozná Pytagorovu vetu, ktorá v matematickom zápise vyzerá nasledovne
a^2 + b^2 = c^2
Ak budem hľadať jej možné riešenia v ktorých sú a, b a c celé čísla, zistíme, že ich už po pomerne krátkom skúmaní nájdeme viacero. Napríklad to môžu byť kombinácie a = 3, b = 4, c =5 či a = 5, b = 12, c = 13
3^2 + 4^2 = 9 + 16 = 5^2 = 25
5^2 + 12^2 = 25 + 144 = 13^2 = 169
5^2 + 12^2 = 25 + 144 = 13^2 = 169
Takýmto trojiciam čísel sa hovorí Pytagorejské trojice a v skutočnosti je ich nekonečné množstvo.
Spýtajme sa či je možné nájsť podobné trojice celých čísel pre rovnicu
a^3 + b^3 = c^3
alebo pre rovnicu
a^4 + b^4 = c^4
alebo všeobecne povedané pre rovnicu
a^n + b^n = c^n kde n je väčšie ako 2.
Toto je otázka nad ktorou rozmýšľal Fermat pri štúdiu latinského prekladu starogréckej zbierky algebraických príkladov, slávnej Diofantovej Aritmetiky. Prišiel s odpoveďou, že to možné nie je. A tvrdil že to vie aj dokázať.
Ako sme už spomenuli, mnoho svojich objavov nedoplnil dôkazom. A tak aj pri skúmaní úloh Diofantovej Aritmetiky si k úlohe zaoberajúcej sa hľadaním Pytagorejských trojíc len pripísal na okraj knihy, poznámku:
Nie je možné rozdeliť kocku do dvoch kociek, či štvrtú mocninu do dvoch štvrtých mocnín alebo všeobecne akúkoľvek mocninu vyššiu ako druhú do dvoch rovnakých mocnín. Objavil som naozaj zvláštny dôkaz tohto tvrdenia, no okraj tejto knihy je primalý na to, aby sa tam vošiel.
Popis dôkazu či len náznak aký dôkaz to bol sa nikdy nenašiel. Vieru že Fermat dôkaz skutočne mal mala na svedomí jeho reputácia fenomenálneho matematika, ktorý podobné tvrdenia bez dôkazu uvádzal bežne, pričom tieto sa neskôr ukázali ako pravdivé. Takýchto tvrdení, spomínajúcich že pozná dôkaz, či len s náznakom ako dôkaz vykonať bolo v komentároch ktoré napísal na okrajoch jeho výtlačku Diofantovej Aritmetiky vyše 20. Všetky boli správne, a všetky boli postupne v relatívne krátkom čase dokázané až na jediné, až na spomenutý problém neexistencie riešenia rovnice a^n + b^n = c^n pre n väčšie ako 2. Tak vzniklo označenie Posledná Fermatova veta. Takto je nazývaná v anglickej literatúre (Fermat's Last Theorem) u nás jej hovoríme Veľká Fermatova veta.
Fermat vytvoril vetu (úlohu), ktorej formulácia je veľmi jednoduchá. Jej dokázanie sa však ukázalo byť viac než zložité a hoc k nemu mnohí prispeli svojou troškou, definitívne riešenie na seba nechalo dlho čakať. Problémom sa zaoberali napríklad Euler, Dirichlet či Legendre ale na dôkaz neprišli. Ako ubiehali roky a ako sa počet tých ktorí sa Fermatovou vetou neúspešne zaoberali zväčšoval, tak rástla výzva a prestíž ktoré jej úspešné vyriešenie sľubovalo.
Mimochodom, ide o úlohu s najväčším počtom nesprávnych riešení v histórii matematiky. A to riešení nielen od matematikov. O jej riešenie sa pokúšali aj tisícky nadšencov, keďže sa predpokladalo, že úloha je riešiteľná matematickými metódami 17. storočia a riešenie je pomerne krátke. Táto pomerná "dostupnosť" a ohromná prestíž ktorá čakala na objaviteľa dôkazu nedala mnohým spať.
Cesta ktorou sa dokazovanie Veľkej Fermatovej vety uberalo je naozaj dlhá, dramatická a spletitá. Tým aj mimoriadne zaujímava, no bohužiaľ niet tu naň miesta, Môžem však skutočne odporúčať knihu Simon Singh - Velká Fermatova věta (Academia, 2007) - http://www.martinus.sk/?uItem=35773 ,ktorá tento príbeh vynikajúco zaznamenáva.
Po tri a pol storočí Veľkú Fermatovu vetu nakonies s pomocou matematiky druhej polovice dvadsiateho storočia dokázal v roku 1994 britský matematik Andrew Wiles. Jeden s najlepších matematikov súčasnosti, strávil jej riešením, v tajnosti, 7 rokov (túto časť, toto finále príbehu Veľkej Fermatovej vety zaznamenáva vynikajúci dokument ktorý pre BBC natočil Simon Singht, autor vyššiespomenutej knihy - dokument si môžete pozrieť na tomto linku: http://video.google.com/videoplay?docid=8269328330690408516). Wilesov dôkaz je extrémne zložitý a dlhý (viď. http://math.stanford.edu/~lekheng/flt/wiles.pdf) a používa metódy enormne vzdialené od tých ktoré mohol poznať Pierre de Fermat. Z toho sa zväčša usudzuje, že Fermat žiaden dôkaz nemal, prípadne že mal chybný dôkaz.
Ale, v mnohých predsa len ešte ostal červík pochybností. Čo ak? Čo ak krátky a jednoduchý dôkaz predsa len existuje.
Naďalej ho mnohí hľadajú.
Ako ste riešili
Reakcie na 1.aprílový žart boli rôzne, od veľmi pozitívnych po veľmi negatívne. Tých negatívnych začalo ubúdať, potom ako s príchodom dnešného rána mnohým začalo dochádzať aký je to dnes deň.
Celkovo sme zaznamenali viac než tisíc pokusov o riešenie ktoré sa delili do nasledujúcich skupín.
1. Úspešné riešenia v tom zmysle že riešitelia vedeli že ide o Veľkú Fermatovu vetu. Vedeli to alebo to vygooglili.
Častokrát sa objavovali kvázisprávne riešenia ako napríklad:
3987^12 + 4365^12 = 4472^12
6,3976656349698612616236230953154e+43 - ľavá strana rovnice 6,3976656348486725806862358322169e+43 - pravá strana rovnice
Ako vidíte, zhoduje sa len prvých 10 miest oboch čísel. Kalkulačka vám ukáže rovnaké čísla, vďaka zaokrúhleniu, ale správne riešenie to nie je. Ide o slávne riešenie ktoré sa objavilo v sitcome Simpsonovci a odvtedy putuje svtom :)
Príjemnýn prekvapením bolo pre nás neznáme kváziriešenie užívateľa hankie (zdroj D. J. Bernstein (July 29, 2001) http://cr.yp.to/threecubes.html)
x = -2901096694
y = -15550555555
z = 15584139827
n = 3
3784848573216710602200773002259 - ľavá strana rovnice
3784848573216710602200773002283 - pravá strana rovnice
Prvých 29 číslic je rovnakých.
V tejto skupine bolo najviac tých ktorí ocenili tento žart. Prvých 50 čitateľov ktorí spoznali že ide o Veľkú Fermatovu vetu dostane od nás sľúbené pero pc.sk a pretaktovanie.sk
Zoznam výhercov :
1). prvým bol krátko po polnoci yesper, ktorý správne napísal "riesenie tejto rovnice podla velkej fermatovej vety neexistuje, samozrejme v mnozine prirodzenych cisel"
2). pEpinko
3). matko86
4). Shigi
5). Lukasko^
6). shigi
7). drahomir.s
8). HellAngel
9). rottenkiwi
10). lukasko
11). zwARO
12). matko86
13). lucky
14). pepe
15). kyleah
16). dmitrijj
17). gabiX
18). spermi
19). avixe
20). Velyger
21). Michal
22). mosqa
23). PROMETHEUS
24). pal0
25). janci2
26). Nightlight
27). Leteku
28). peYko
29). nexus33
30). jatmz
31). louth
32). predator
33). latigi
34). Thunderbolt
35). pacho666
36). ddussann
37). mirak
38). Maxx
39). frcko
40). Tom.raketa
41). risomas
42). Blackhawk
43). edt
44). matej1982
45). powerarm
46). Seky
47). mastro
48). gyver
49). Phalanx
50). chosefina
2. Riešitelia pokúšajúci sa nájsť riešenie. Mnohí z nich pochopili že rovnica má nulové riešenie, to však zadanie vylučovalo. Postupne intuitívne pochopili že pôjde o nejaký žart, alebo že rovnica asi riešenie mať nebude.
3. Tí ktorí to vzdali hneď na začiatku
4. Nahnevaní čitatelia. Sme radi že pozitívne reakcie prevažovali, ale pár nahnevaných reakcií stálo za to.
Napríklad :
Užívateľ lordjustice a jeho poznámka: "Komentár je ten, že kto vymyslel túto hovadinu, tak by nemal dostať výplatu!!!". Milý lord spravodlivosti, chceme Ťa uistiť, že za tento nápad, jeho prípravu, či za tento článok nik honorár nedostane :)
5. Srandisti a tí ostatní
Informatik sa nezaprel: baqq:
x = 8
y = 8
z = 10
n = 3
Poznamka: 512+512 = sice 1024, ale v bitoch je to 1000, cize 10 na 3.
Anonym: Poznamka: Kdybych tohle umel vyresit, tak nechodim na pc.sk. ;-)
My dodáme, že súhlasíme, že dokazat Fermatovu vetu vie len zopar ľudí na svete a je to úctyhodný výkon. Taký čo to, vie by kvoli Porche, jachte na ceste okolo sveta a frajerke čo vyhrala miss minulý rok nemal mať na pc.sk čas :)
lamzalo fermat by sa v hrobe obracal ze ho zneuzili na prvy april :-D
fawrell - potom čo správne vysvetlil že riešenie neexistuje poznamenal "S googlom sa stal zivot prilis lahkym. Jedina vec na uvazovanie bola, ako zadat do googla "x na n-tu". Ale s tym si iste poradila vacsina ludi. Dalej je to uz len o googli. Co by ludia robili bez googla ..."
Tak, hádam aj tí nahnevaní majú tú trošku zmyslu pre humor, a tento náš 1. apríl nejako strávia :)

GABO
Gudas
Pavol Bobik
GABO
zwARO
marto
pEpinko
stryk0
matko86
ddussann
dendroid
shigi
Velyger
Velyger
Hrochy
Pavol Bobik
vacropoli
neo140
neo140
Satano
thundabird
Pavol Bobik
vacropoli
thundabird
vacropoli
4ngel
lacikaboss
M1ch4l
vacropoli
Marthinez
lordjustice2
4ngel
amd_sk
k0rben
GABO
lordjustice2
Pavol Bobik
k0rben
GABO
GABO
k0rben
lordjustice2